After Tossing the Same Coin 10 Times

After tossing the same coin 10 times you are surprised to find that tails has come up 8 times. If you toss a coin 10 times and it lands heads up every time what are the chances it will land heads up if you toss it again.

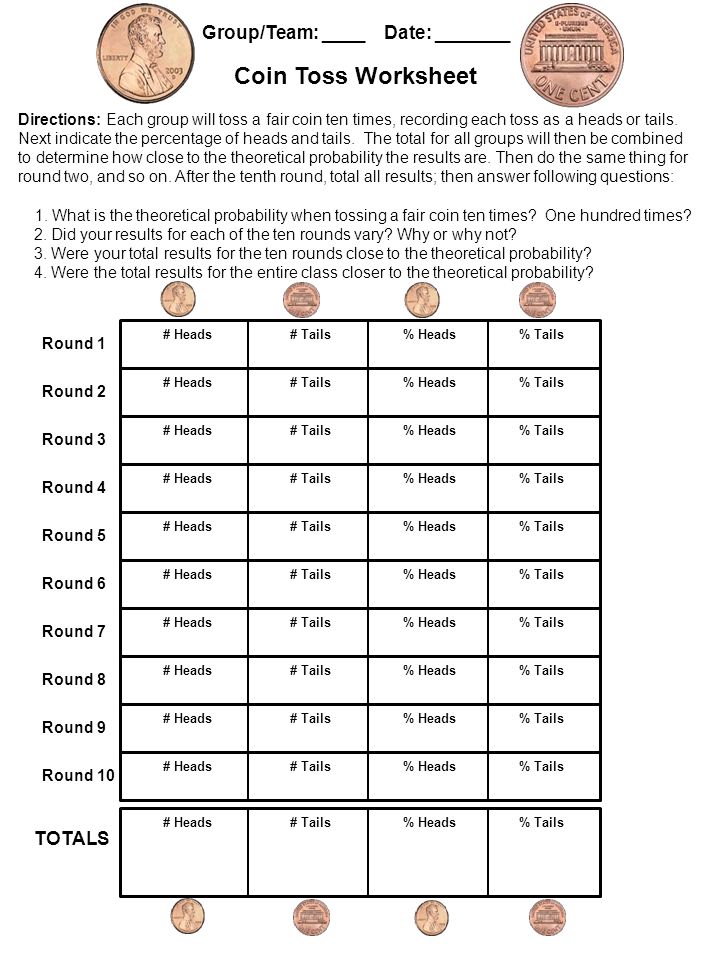
Probability A Coin Toss Activity Directions Each Group Will Toss A Fair Coin Ten Times On The Worksheet They Will Record Each Toss As A Heads Or Tails Ppt Download

Identify the following probability as theoretical or empirical.

. After tossing the same coin 10 times you are surprised to find that tails has come up 8 times. It may be that you dont have a fair coin or it might just be chance. Empirical apex students xp.

This means Total observations 2 5 According to binomial concept Required outcome 5 Heads HHHHH This can occur only ONCE. After tossing the same coin 10 times you are surprised to find that tails has come up 9 times You therefore conclude that this coin is not fair and that the probability of getting tails with this co. Identify the following probability as theoretical or empirical.

After tossing a coin there are 2 possible outcomes ie. We denote Head as H and Tail as Tail. The previous toss does not impact the next toss.

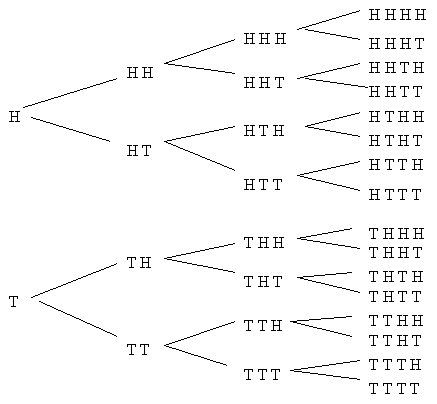
Let X be the random variable that is the number of heads in the outcome. 6 How many different outcomes have exactly 5 Heads and 5 Tuils. Ways of choosing 7 from remaining 7 7C7 1.

If youre looking to use the conditional probability formula you can. The outcomes of the event of tossing multiple coins would be the same as the outcomes of tossing a coin multiple times and collecting the outcomes. When a coin is tossed either head or tail shows up.

There is a 5050 chance of each toss being either heads or tails. Which is to say how many the base 2 is multiplied by its self - 10. Question 5 A coin is tossed 10 times and the result of Heads or This is recorded after each toss a Since the order of H or T matters when we are recording them in order how many different outcomes are possible.

Now favourable outcome is 3 heads 7 tails. N k p k 1 p n k. The number of possible choices in.

After tossing the same coin 10 times you are surprised to find that tails has come up 9 times You therefore conclude that this coin is not fair and that the probability of getting tails with this co. Every coin has two sides. The set of all possible outcomes of a random experiment is known as its sample spaceThus if your random experiment is tossing a coin then the sample space is Head Tail or more succinctly H TIf the coin is fair which means that no outcome.

After tossing the same coin 10 times you are surprised to find that tails has come up 9 times You therefore conclude that this coin is not fair and that the probability of getting tails with this co. I should know Ive seen at least one of each Well let me explain that these two problems are basically the same that is from the point of view of mathematicsWhether you want to toss a coin or ask a girl out there are only two possibilities that can occurIn other words if you assign the success of your. 1024 2 possibile coin outcomes per flip 10 number of flips 2 is the base and 10 is the power to which it is raised.

Hey man but girls and coins are two different things. The probability of getting exactly one head regardless of where is 10 1024. If a coin is tossed 5 times what is the probability that it will always land on the same side.

If we toss a coin n times and the probability of a head on any toss is p which need not be equal to 1 2 the coin could be unfair then the probability of exactly k heads is. Problem 2 20 pts. Problem 1 10 pts.

The idea can be substantially generalized. As you toss a coin 10 times obviously n S 210. Tossing a coin 3 times would be the same as tossing a coin thrice.

You therefore conclude that this coin is not fair and that the probability of getting tails with this coin is 080. You therefore conclude that this coin is not fair and that the probability of getting tails with this coin is 070. The probability formula for a coin flip can be used to calculate the probability of some experiment.

210 Eleven flips would be 211 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X flip. Let us assume that after flipping 5 coins we get 5 heads in result. You therefore conclude that this coin is.

As according to the question when 10 coins are tossed then 210 1024 is the answer. And when 2 coins are tossed then there are 4 outcomes ie. C How many different outcomes have at least 7 Heads.

Finding Number of possible choices A coin tossed has two possible outcomes showing up either a head or a tail. After tossing the same coin 10 times you are surprised to find that tails has come up 8 times You therefore conclude that this coin is not fair and that the probability of getting tails with this co. This is one out of 1024 possible outcomes so its probability is 1 1024.

After tossing the same coin 10 times you are surprised to find that tails has come up 7 times. There is one way to get exactly one head on the first toss of 10. H T T T T T T T T T.

Find the mean and variance of X. N 5 balls are thrown into m 2 bins numbered 12m uniformly at random ie for each ball you toss it into a bin chosen uniformly at random from the m bins. It may be that you dont have a fair coin or it might just be chance.

Probability 120210 1523210 1527 15128. Answer 1 of 9. Ways of choosing 7 from 10 10C7 120.

An experiment consists of tossing a coin 6 times. The simple formula for this is 2n where n is the number of times the coin is tossed. So the probability of exactly 3 heads in 10 tosses is 120 1024.

This page discusses the concept of coin toss probability along with the solved examples. 22 and so on. Tossing a coin on the other hand is a random experiment since you know the set of outcomes but not the exact outcome for each random experiment execution.

Likely Events Never Happen

Example 31 If A Fair Coin Is Tossed 10 Times Find Probability

That Common Misconception About Probability By Brett Berry Math Hacks Medium

Share this post